


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie
... ... ...
 |
 |


... ... ...
...
| Les nombres décimaux | Les fractions |
|
Définition Écriture des décimaux Lecture des décimaux Écriture fractionnaire |
Définition Des fractions courantes Transformer des fractions |

...
Définition - Généralités
...
Une baguette de pain coûte 0,75 € ; elle pèse 0,25 kilogramme.
La Renault 5 consomme 5,4 litres d’essence aux 100 kilomètres.
L’envergure de l’avion Concorde est égale à 25,56 mètres.
=> Les nombres 0,75 ; 0,25 ; 5,4 et 25,56 sont des nombres décimaux.
...
- Un nombre décimal s’écrit avec les chiffres 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9 , et une virgule.
- Les chiffres situés à gauche de la virgule constituent la partie entière du nombre décimal.
- Les chiffres situés à droite de la virgule constituent la partie décimale de ce nombre.
La virgule sépare les chiffres de ces 2 groupes.
...
- Comme pour la partie entière, la position des chiffres de la partie décimale définit leur valeur :
- le premier chiffre derrière la virgule est le chiffre des dixièmes ;
- le deuxième chiffre derrière la virgule est le chiffre des centièmes ;
- le troisième chiffre derrière la virgule est le chiffre des millièmes…
...
Dans le tableau suivant, tu trouveras la classe de chaque chiffre pour quelques nombres décimaux :
0,75 / 5,4 / 25,56 / 123,456
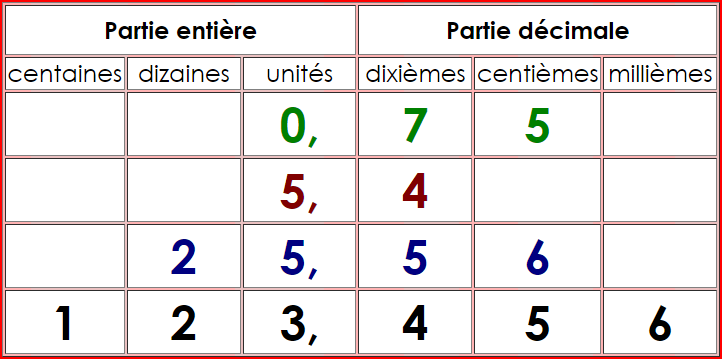
Remarques :
- On écrit un seul chiffre par case dans le tableau.
- On n’écrit pas de zéros à droite de la dernière décimale non nulle.
- Quand tous les chiffres de la partie décimale sont des zéros, on n’écrit pas les zéros de la partie décimale, ni même la virgule : le nombre est un nombre entier naturel.
...
Exemple :
Soit le nombre 123,456
La partie entière est composée des chiffres 1 , 2 et 3
1 est le chiffre des centaines
2 est le chiffre des dizaines
3 est le chiffre des unités
La partie décimale est composée des chiffres 4 , 5 et 6
4 est le chiffre des dixièmes
5 est le chiffre des centièmes
6 est le chiffre des millièmes
...
Le tableau de numération
...
Pour lire les nombres décimaux, on lit la partie entière, puis on ajoute le mot « virgule » et on lit ensuite la partie décimale en précisant la présence des zéros intercalés, si besoin.
Ou bien on peut lire le nombre en précisant la valeur des chiffres ou des nombres.
Pour les nombres indiquant des unités de mesure, on énonce le nom de l'unité à la place de la virgule.
Exemples :
8,092 : huit virgule zéro quatre-vingt-douze (ou huit unités et quatre-vingt-douze millièmes)
25,43 : vingt-cinq virgule quarante-trois (ou vingt-cinq unités et quarante-trois centièmes)
0,004 : zéro virgule zéro zéro quatre (ou quatre millièmes)
2,75 € : deux virgule soixante-quinze euros (ou deux euros soixante-quinze)
25,56 m : vingt-cinq virgule cinquante-six mètres (ou vingt-cinq mètres cinquante-six)
...
...
...
0,1
1 un dixième |
0,01
1 un centième |
0,001
1 un millième |
Tous les nombres décimaux peuvent s'écrire sous forme d'une fraction décimale.
Une fraction décimale est une fraction dont le numérateur est un nombre entier et dont le dénominateur est 10 , 100 ou 1 000...
Exemples :
| 47,3 = |
473 10 |
...
| 25,43 = |
2 543 100 |
...
| 0,007 = |
7 1 000 |
...
Et pour trouver le nombre décimal représenté par une fraction décimale, il suffit de diviser son numérateur (nombre du haut) par son dénominateur (nombre du bas : 10 ; 100 ; 1 000…)
Exemples :
|
5 10 |
= 5 : 10 = 0,5 et se lit "cinq dixièmes" (ou "zéro unité et cinq dixièmes") |
...
|
15 100 |
= 15 : 100 = 0,15 et se lit "quinze centièmes" (ou "zéro unité et quinze centièmes") |
...
|
7 1 000 |
= 7 : 1 000 = 0,007 et se lit "sept millièmes" (ou "zéro unité et sept millièmes") |
Remarques :
| 3,5 | = |
35 10 |
= |
350 100 |
= |
3 500 1 000 |
...
|
1 10 |
= 1 : 10 = 0,1 |
=> Diviser un nombre par dix revient donc à le multiplier par 0,1
Exemple :
| 587 : 10 = |
587 10 |
= 587 x 0,1 = 58,7 |
...
... ... ...
...
On utilise souvent des fractions :
|
1 2 |
dans une "demi-baguette" |
...
|
3 4 |
dans "trois quarts d'heure" |
...
|
1 100 |
dans un "centième de seconde" |
...
Une fraction est en fait une division.
|
A B |
= A : B |
...
| A | => | le numérateur |
| _____ | => | la barre de fraction |
| B | => | Le dénominateur |
Le numérateur indique le nombre total (le dividende) de parties utilisées .
Le dénominateur indique en combien de parties (le diviseur) on divise l’objet, le prix, la quantité...
Pour lire une fraction, on lit d'abord le nombre du numérateur, puis le nombre du dénominateur en ajoutant le suffixe "ième".
(Mais il existe des exceptions : demi, tiers et quart)
Exemple :
|
9 11 |
se lit "neuf onzièmes" |
...
...
- Une fraction est égale à 1 si le numérateur et le dénominateur sont égaux.
Exemples :
|
8 8 |
= 1 |
10 10 |
= 1 |
35 35 |
= 1 |
...
- Une fraction peut être égale à un nombre entier.
Si le numérateur est divisible par le dénominateur, alors la fraction est égale à un nombre entier.
Exemples :
|
8 4 |
= 2 |
9 3 |
= 3 |
12 3 |
= 4 |
...
- Deux fractions différentes peuvent être égales.
Si on multiplie ou si on divise le numérateur et le dénominateur d'une fraction par un même nombre, alors on obtient une fraction égale.
Exemples :
|
2 3 |
= |
2 x 3 3 x 3 |
= |
6 9 |
|
15 10 |
= |
15 : 5 10 : 5 |
= |
3 2 |
...
- Simplifier des fractions
Si le numérateur et le dénominateur sont divisibles par un même nombre, alors on peut simplifier la fraction en divisant le numérateur et le dénominateur par ce nombre, et les deux fractions restent égales.
Exemple :
|
12 64 |
= |
6 x 2 32 x 2 |
= |
6 32 |
= |
3 x 2 16 x 2 |
= |
3 16 |
...
- Comparer des fractions
Pour comparer des fractions entre elles, il peut être utile de transformer les fractions afin qu’elles aient le même dénominateur. Il suffit alors de comparer les numérateurs.
Exemple :
|
3 4 |
et |
2 3 |
? => |
3 4 |
= |
9 12 |
et |
2 3 |
= |
8 12 |
=> 9 > 8 donc |
3 4 |
> |
2 3 |
...
- Évaluer l'ordre de grandeur des fractions
Si le numérateur est plus petit que le dénominateur, alors la fraction est inférieure à 1.
Si le numérateur est plus grand que le dénominateur, alors la fraction est supérieure à 1.
Si le numérateur et le dénominateur sont égaux, la fraction est égale à 1.
Exemples :
|
75 100 |
< 1 |
100 75 |
> 1 |
75 75 |
= 1 |
Pour transformer les fractions, il est indispensable de maîtriser les tables de multiplication et de connaître les critères de divisibilité.
Les tables de multiplication (Niveau 2)
Les critères de divisibilité (Niveau 3)
...
... ... ...
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le cycle 3 en mathématiques
CM1 - CM2
Numération - Les nombres décimaux - Les fractions