


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie - Repérage
... ... ...
 |
 |


... ... ...
...
| Addition | Soustraction |
|
Technique opératoire Les tables d'addition Synthèse |
Technique opératoire La preuve Synthèse |
| Multiplication |
|
Les tables de multiplication Technique opératoire Synthèse |

...
L’opération qui sert à calculer une somme entre 2 nombres est l’addition.
Exemple :
Pierre rentre de l’école avec 24 billes dans sa trousse.
Il en gagne 7 pendant la récréation.
...
Pour trouver combien il a de billes en tout, il faut effectuer l’addition « 24 + 7 ».
On écrit :
| Opération en ligne : | Opération en colonnes : | |
| 24 + 7 = 31 |
12 4 + 7 3 1 |
|
...
C'est ici !...
...
Technique opératoire : l'addition en colonnes

...
Exemples :
- Sans retenue :
| 35 + 41 = ? | 35 + 41 = ? | 35 + 41 = ? | |||
|
3 5 + 4 1 ? ? |
|
3 5 + 4 1 ? 6 |
5 + 1 = 6 |
3 5 + 4 1 7 6 |
3 + 4 = 7 |
- Avec retenue :
| 57 + 84 = ? | 57 + 84 = ? | 57 + 84 = 141 | |||
|
5 7 + 8 4 ? ? |
|
15 7 + 8 4 ? 1 |
7 + 4 = 11 |
15 7 + 8 4 1 4 1 |
1 + 5 + 8 = 14 |
...
Remarques :
- On peut inverser l’ordre des nombres :
20 + 10 = 10 + 20 = 30
- « 0 » est un nombre neutre (il ne change rien) :
20 + 0 = 0 + 20 = 20
...
- Aligner correctement les 2 nombres.
- Commencer par la droite en additionnant les chiffres des unités.
- Faire attention aux retenues !...
| Addition posée en ligne : | Addition posée en colonnes : | |
|
Attention aux retenues !... 123 + 89 = 212 |
Attention à l’alignement !... Attention aux retenues !... |
1112 3 + 8 9 2 1 2 |
...

...
... ... ...
...
L’opération qui sert à calculer une différence entre 2 nombres est la soustraction.
Exemple :
Pierre a 38 billes dans sa trousse.
Il en donne 10 à son petit frère.
...
Pour trouver combien il a de billes, il faut effectuer la soustraction « 38 – 10 ».
On écrit :
| Opération en ligne : | Opération en colonnes : | |
| 38 - 10 = 28 |
3 8 - 1 0 2 8 |
|
...
Technique opératoire : la soustraction en colonnes

...
2 cas peuvent se produire :
- Sans retenue :
| 35 - 21 = ? | 35 - 21 = ? | 35 - 21 = 14 | |||
|
3 5 - 2 1 ? ? |
|
3 5 - 2 1 ? 4 |
3 5 - 2 1 1 4 |
||
- Avec retenue :
| 51 - 25 = ? | 51 - 25 = ? | ||
|
5 1 - 2 5 ? ? |
1 - 5 ? Ce n'est pas possible... |
(+10) 5 1 - (+1)2 5 ? 6 |
J'obtiens : 11 - 5 = 6 |
| 51 - 25 = 26 |
(+10) 5 1 - (+1)2 5 2 6 |
J'obtiens : 5 - (2 + 1) 5 - 3 = 2 |
Si j’ajoute le même nombre aux 2 termes de la soustraction, le résultat reste le même.
J’ajoute donc 10 unités au nombre du haut, et 1 dizaine au nombre du bas.
...
C'est ici !...
...
Pour vérifier le résultat d'une soustraction, on peut calculer l'addition associée.
On peut facilement vérifier le résultat d’une soustraction en calculant l'addition associée : il suffit d'ajouter le résultat obtenu au nombre retranché (le plus petit).
Si l'on retrouve le nombre de départ (le plus grand), alors la soustraction est juste.
Exemples :
8
- 5 = 3
=>
3 + 5 = 8
250
- 84 = 166
=>
166 + 84 = 250
5 000
- 2 550 = 2 450
=>
2 450 + 2 550 = 5 000
...
- Placer en haut le nombre le plus grand. (le total)
- Placer en dessous le nombre le plus petit. (ce qu’on enlève)
- Aligner correctement les 2 nombres.
- Commencer par la droite en soustrayant les chiffres des unités, puis les chiffres des dizaines...
| Soustraction posée en ligne : | Soustraction posée en colonnes : | |
|
Attention aux retenues ! 123 - 89 = 34 |
Attention à l’alignement ! Attention aux retenues ! |
11213 - 118 9 0 3 4 |
- La preuve de la soustraction :
|
18 9 + 3 41 2 3 |
...
...
... ... ...
...
L’opération qui sert à calculer un produit entre 2 nombres est la multiplication.
Exemple :
La maîtresse de Pierre distribue 4 cahiers à chacun des 27 élèves.
...
Pour trouver combien de cahiers elle a distribués, il faut effectuer la multiplication "4 x 27"
On écrit :
| Opération en ligne : | Opération en colonnes : | |
| 4 x 27 = 108 |
22 7 x 4 1 0 8 |
|
...
Remarques :
- La multiplication est équivalente à une succession d'additions du même nombre :
4 + 4 + 4 + 4 + 4 + 4 = 6 x 4
- On peut inverser l'ordre des nombres :
3 x 5 = 5 x 3 = 15
- "1" est un élément neutre (il ne change rien)
8 x 1 = 1 x 8 = 8
- "0" est une élément absorbant (le résultat est toujours égal à 0)
10 x 0 = 0 x 10 = 0
...
| "0" | "1" |
|
0 x 0 = 0 0 x 1 = 0 0 x 2 = 0 0 x 3 = 0 0 x 4 = 0 0 x 5 = 0 0 x 6 = 0 0 x 7 = 0 0 x 8 = 0 0 x 9 = 0 0 x 10 = 0 |
1 x 0 = 0 1 x 1 = 1 1 x 2 = 2 1 x 3 = 3 1 x 4 = 4 1 x 5 = 5 1 x 6 = 6 1 x 7 = 7 1 x 8 = 8 1 x 9 = 9 1 x 10 = 10 |
...
| "2" | "3" |
|
2 x 0 = 0 2 x 1 = 2 2 x 2 = 4 2 x 3 = 6 2 x 4 = 8 2 x 5 = 10 2 x 6 = 12 2 x 7 = 14 2 x 8 = 16 2 x 9 = 18 2 x 10 = 20 |
3 x 0 = 0 3 x 1 = 3 3 x 2 = 6 3 x 3 = 9 3 x 4 = 12 3 x 5 = 15 3 x 6 = 18 3 x 7 = 21 3 x 8 = 24 3 x 9 = 27 3 x 10 = 30 |
...
| "6" | "7" |
|
4 x 0 = 0 4 x 1 = 4 4 x 2 = 8 4 x 3 = 12 4 x 4 = 16 4 x 5 = 20 4 x 6 = 24 4 x 7 = 28 4 x 8 = 32 4 x 9 = 36 4 x 10 = 40 |
5 x 0 = 0 5 x 1 = 5 5 x 2 = 10 5 x 3 = 15 5 x 4 = 20 5 x 5 = 25 5 x 6 = 30 5 x 7 = 35 5 x 8 = 40 5 x 9 = 45 5 x 10 = 50 |
...
| "6" | "7" |
|
6 x 0 = 0 6 x 1 = 6 6 x 2 = 12 6 x 3 = 18 6 x 4 = 24 6 x 5 = 30 6 x 6 = 36 6 x 7 = 42 6 x 8 = 48 6 x 9 = 54 6 x 10 = 60 |
7 x 0 = 0 7 x 1 = 7 7 x 2 = 14 7 x 3 = 21 7 x 4 = 28 7 x 5 = 35 7 x 6 = 42 7 x 7 = 49 7 x 8 = 56 7 x 9 = 63 7 x 10 = 70 |
...
| "8" | "9" |
|
8 x 0 = 0 8 x 1 = 8 8 x 2 = 16 8 x 3 = 24 8 x 4 = 32 8 x 5 = 40 8 x 6 = 48 8 x 7 = 56 8 x 8 = 64 8 x 9 = 72 8 x 10 = 80 |
9 x 0 = 0 9 x 1 = 9 9 x 2 = 18 9 x 3 = 27 9 x 4 = 36 9 x 5 = 45 9 x 6 = 54 9 x 7 = 63 9 x 8 = 72 9 x 9 = 81 9 x 10 = 90 |
...
| "10" |
|
10 x 0 = 0 10 x 1 = 10 10 x 2 = 20 10 x 3 = 30 10 x 4 = 40 10 x 5 = 50 10 x 6 = 60 10 x 7 = 70 10 x 8 = 80 10 x 9 = 90 10 x 10 = 10 |
...
... ... ...
On peut également utiliser le tableau ci-dessous pour connaître le résultat des multiplications ave les nombres de 0 à 10.
On trouve le résultat au croisement des lignes et colonnes correspondants aux nombres choisis.
Ce tableau s'appelle la table de Pythagore.
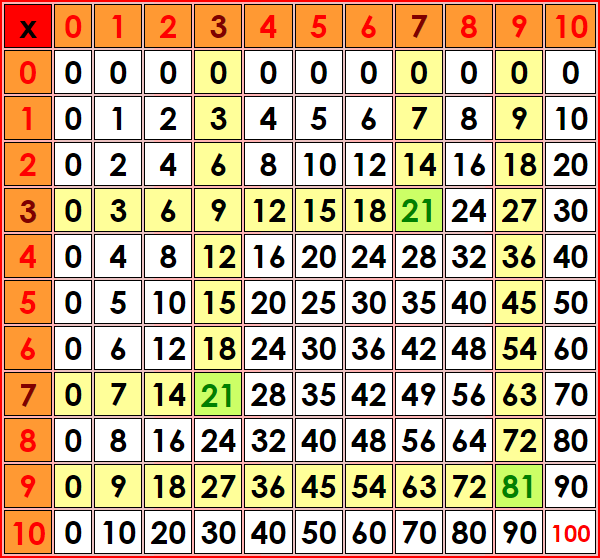
Exemples :
7 x 3 = 3 x 7 = 21
9 x 9 = 81
...
...
Technique opératoire : la multiplication en colonnes

...
- Sans retenue :
| 34 x 2 = ? | 34 x 2 = ? | 34 x 2 = 68 | |||
|
3 4 x 2 ? ? |
3 4 x 2 ? 8 |
2 x 4 = 8 |
3 4 x 2 6 8 |
2 x 3 = 6 | |
- Avec retenue :
| 34 x 5 = ? | 34 x 5 = ? | 34 x 5 = 170 | |||
|
3 4 x 5 ? ? |
23 4 x 5 ? 0 |
5 x 4 = 20, je pose 0 et je retiens 2 |
23 4 x 5 1 7 0 |
5 x 3 = 15 15 + 2 = 17 |
|
...
- Aligner correctement les 2 nombres...
- Commencer par la droite en multipliant les chiffres des unités, puis celui des dizaines...
- Faire attention aux retenues !...
...
| Multiplication posée en ligne : | Multiplication posée en colonnes : | |
|
Attention aux retenues ! 46 x 4 = 184 |
Attention à l’alignement ! Attention aux retenues ! |
24 6 x 4 1 8 4 |
... ... ...
 |
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le Cycle 2 en mathématiques
CE1 - CE2
Calcul - Addition - Soustraction - Multiplication