


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie
... ... ...
 |
 |


... ... ...
...

...
...
Pour effectuer une addition avec des nombres décimaux, on utilise les mêmes règles qu’avec les nombres entiers.
Pour le calcul en colonnes, il faut juste aligner les nombres correctement en plaçant les chiffres de même nature (centaine, dizaine, dixième, centième…) les uns sous les autres ; et ne pas oublier d’ajouter une virgule au résultat en l’alignant également.
Si besoin, il peut être utile d’ajouter des zéros, voire de transformer un nombre entier en nombre décimal.
Exemples :
| 17,45 + 64,6 = 82,05 | 8,605+ 9 = 17,605 | ||
|
1117, 4 5 + 6 4, 6 0 8 2, 0 5 |
8,6 0 5 + 9, 0 0 0 1 7, 6 0 5 |
||
Enfin, il est souvent utile d’évaluer l’ordre de grandeur du résultat afin de vérifier son résultat.
...
Calculer une addition en colonnes avec des nombres décimaux
...
Exercices en lignes :
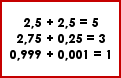 |
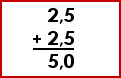 |
... ... ...
...
Pour effectuer une soustraction avec des nombres décimaux, on utilise les mêmes règles qu’avec les nombres entiers.
Pour le calcul en colonnes, il faut juste aligner les nombres correctement en plaçant les chiffres de même nature (centaine, dizaine, dixième, centième…) les uns sous les autres ; et ne pas oublier d’ajouter une virgule au résultat en l’alignant également.
Si besoin, il peut être utile d’ajouter des zéros, voire de transformer un nombre entier en nombre décimal.
Exemples :
| 84,85 - 5,3 = 79,55 | 8 - 2,325 = 5,675 | ||
|
814,8 5 - 1 5, 3 0 7 9, 5 5 |
8,101010 - 12,1312 5 5, 6 7 5 |
||
Enfin, il est souvent utile d’évaluer l’ordre de grandeur du résultat afin de vérifier son résultat.
...
Calculer une soustraction en colonnes avec des nombres décimaux
...
Exercices en lignes :
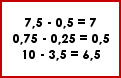 |
 |
... ... ...
...
Pour effectuer une multiplication avec des nombres décimaux, on utilise les mêmes règles qu’avec les nombres entiers.
Pour le calcul en colonnes, on effectue le produit sans tenir compte de la virgule. On place ensuite la virgule de façon à ce que le résultat ait le même nombre de décimales que les termes du produit.
Exemples :
| Multiplication d'un décimal par un entier :
85,64 x 27 = 2 312,28 |
Multiplication de deux décimaux :
0,255 x 8,6 = 2,1930 |
||
|
8 5, 6 4 x 2 7 5 9 9 4 8 + 1 7 1 2 8 0 2 3 1 2,2 8 |
2 / 4 / 3 1 / 1 |
0, 2 5 5 x 8, 6 1 5 3 0 + 2 0 4 0 0 2,1 9 3 0 |
3 / 3 / 1 4 / 4 / 2 |
...
Calculer une multiplication en colonnes avec des nombres décimaux
...
Pour multiplier un nombre décimal par 10, 100, 1 000… , on déplace la virgule d’1, 2, 3… rangs vers la droite. On peut ajouter des zéros si nécessaire.
Exemples :
35,641 x 10 = 356,41
35,641 x 100 = 3 564,1
35,641 x 1 000 = 35641
...
35,6 x 10 = 356
35,6 x 100 = 3 560
35,6 x 1 000 = 35 600
...
Pour multiplier un nombre décimal par 0,1 , 0,01 , 0,001 ,… , on déplace la virgule d’1, 2, 3… rangs vers la gauche.
Exemples :
345 x 0,1 = 34,5
345 x 0,01 = 3,45
345 x 0,001 = 0,345
...
234,5 x 0,1 = 23,45
234,5 x 0,01 = 2,345
234,5 x 0,001 = 0,2345
...
...
Exercices en lignes :
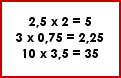 |
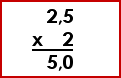 |
... ... ...
...
Il suffit de déplacer la virgule d’1, 2 ou 3 rangs vers la gauche du nombre et de supprimer éventuellement les zéros inutiles.
Exemples :
...
...
...
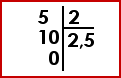
Lorsque le reste est différent de zéro, on peut continuer la division en utilisant les nombres décimaux. Il faut abaisser un zéro à la suite du reste et placer une virgule derrière le dernier chiffre du quotient entier, qui devient donc un nombre décimal.
On peut alors abaisser autant de 0 que l’on veut… jusqu’à obtenir un reste égal à zéro. Mais attention, certaines divisions sont « infinies » !
Exemples :
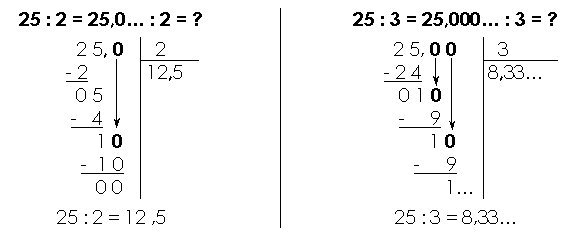
...
Il suffit de placer une virgule au quotient lorsque l’on arrive au niveau de la virgule du dividende. On peut bien sûr ajouter des zéros à la droite de la partie décimale du dividende.
Exemples :
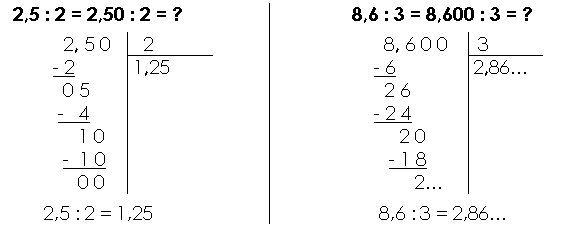
...
Calculer une division en colonnes avec des nombres décimaux
...
Exercices en lignes :
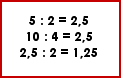 |
 |
...
... ... ...
...
...
La moyenne se calcule en additionnant tous les termes dont on souhaite effectuer une moyenne (à condition que la série de nombres soit cohérente !), puis en les divisant par le nombre de termes.
Exemple :
- 16 élèves d’une classe de CM2 ont participé à un « défi mathématiques ». Voici les notes qu’ils ont obtenues :
11 - 17 - 11 - 15 - 12 - 9 - 12 - 8 - 14 - 15 - 13 - 17 - 17 - 16 - 14 - 16
Pour calculer la moyenne obtenue par ces élèves à ce défi, on doit effectuer les calculs suivants :
- Calculer la somme des notes obtenues :
11 + 17 + 11 + 15 + 12 + 9 + 12 + 8 + 14 + 15 + 13 + 17 + 17 + 16 + 14 + 16 =
(11 x 2) + (17 x 3) + (15 x 2) + (12 x 2) + (14 x 2) + (16 x 2) + 9 + 8 + 13 =
[(11 + 15 + 12 + 14 + 16) x 2] + (17 x 3) + 9 + 8 + 13 =
(68 x 2) + 51 + 9 + 8 + 13 =
136 + 60 + 21 = 217
- Diviser le total obtenu par le nombre de notes :
217 : 16 = 13,56...
La moyenne de la classe au défi mathématiques est donc de 13,5.
...
... ... ...
...
- Pour effectuer des calculs entre des nombres entiers et des fractions décimales, le plus simple est d’écrire les fractions sous la forme du nombre décimal équivalent.
Exemples :
| 5 + |
25 10 |
= 5 + 2,5 = 7,5 |
...
| 14 - |
35 100 |
= 14 - 0,35 = 13,65 |
...
| 25 x |
5 10 |
= 25 x 0,5 = 12,5 |
...
| 35 : |
5 10 |
= 35 : 0,5 = 70 |
...
- Pour effectuer des additions ou des soustractions avec des fractions décimales, si les dénominateurs sont égaux, il suffit d’effectuer les calculs entre les numérateurs.
Si les dénominateurs sont différents, il faut transformer les fractions afin d’obtenir le même dénominateur pour les différentes fractions.
Exemples :
|
35 100 |
+ |
15 100 |
= |
35 + 15 100 |
= |
50 100 |
= |
1 2 |
...
|
8 10 |
+ |
75 100 |
= |
80 100 |
+ |
75 100 |
= |
155 100 |
= |
31 20 |
...
|
8 10 |
- |
2 10 |
= |
8 - 2 10 |
= |
6 10 |
= |
3 5 |
...
|
9 10 |
- |
54 100 |
= |
90 100 |
- |
54 100 |
= |
36 100 |
= |
9 25 |
...
- Pour effectuer des multiplications entre fractions décimales, il suffit simplement de multiplier les numérateurs entre eux et les dénominateurs entre eux. On obtient une nouvelle fraction décimale… Attention aux zéros !…
|
3 10 |
x |
5 10 |
= |
3 x 5 10 x 10 |
= |
15 100 |
= |
3 20 |
...
|
5 10 |
x |
25 100 |
= |
5 x 25 10 x100 |
= |
125 1 000 |
= |
1 8 |
...
- Pour effectuer des divisions entre fractions décimales, il faut inverser le numérateur et le dénominateur de la fraction décimale qui sert de diviseur… et de procéder comme si c’était une multiplication !…
|
9 10 |
: |
3 10 |
= |
9 10 |
x |
10 3 |
= |
90 30 |
= | 3 |
...
|
5 10 |
: |
25 100 |
= |
5 10 |
x |
100 25 |
= |
500 250 |
= | 2 |
...
... ... ...
...
...
Deux suites de nombres sont proportionnelles quand on passe de l’une à l’autre en multipliant ou en divisant les nombres d’une suite par un même nombre, et que l’on obtient les nombres de la seconde suite.
Exemple :
- Pour éviter de calculer à chaque fois le montant à encaisser quand elle vend des sucettes, une boulangère a dressé le tableau suivant :
(le prix d’une sucette est de 0,75 €)
| Nombre de sucettes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix correspondant en € | 0,75 | 1,50 | 2,25 | 3,00 | 3,75 | 4,50 | 5,25 | 6,00 | 6,75 | 7,50 |
- Pour obtenir les nombres de la deuxième ligne du tableau (les prix des sucettes), elle a multiplié les nombres de la première ligne par 0,75 (soit le prix d'une seule sucette).
- On dit que la suite des nombres de la première ligne est proportionnelle à la suite des nombres de la deuxième ligne.
0,75 est le coefficient de proportionnalité ou l’opérateur qui permet de passer de la première ligne à la seconde.
Si la situation est proportionnelle et que l’on trace un graphique associant les données, tous les points sont alignés :
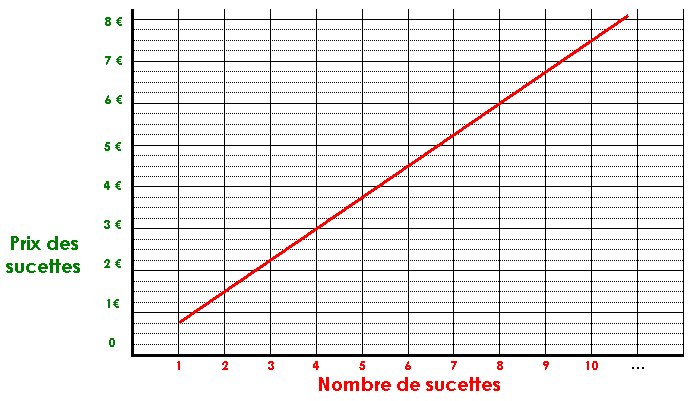
...
Il existe 2 situations particulières pour lesquelles la proportionnalité intervient : les pourcentages et les échelles.
... ... ...
...
- L’échelle indique la proportion entre les mesures réelles et les mesures représentées sur des cartes, des plans, des images, des maquettes... Ces objets sont des représentations de la réalité diminuée (ou agrandie) de façon proportionnelle.
L’échelle constitue le coefficient de proportionnalité.
Une maquette à l’échelle 1 : 20 (on lit un vingtième), signifie que la taille réelle de l’objet a été réduite 20 fois.
Exemple :
- On souhaite représenter sur un plan un terrain de football en réduisant 500 fois les dimensions du terrain. L’échelle est donc de 1 : 500 (un cinq centièmes) et signifie que sur mon plan 1 cm sera équivalent à 500 centimètres (soit 5 mètres) de la réalité.
(Les dimensions réelles d’un terrain de football sont de 110 m de long et 65 m de large.)
- Les dimensions sur le plan seront donc :
Longueur du terrain sur le plan :
110 : 500 = 0,22 m (soit 22 cm)
Largeur du terrain sur le plan :
65 : 500 = 0,13 m (soit 13 cm)
...
Quand on opère des calculs avec des échelles, il faut faire très attention à exprimer les deux grandeurs (réelles et représentées) dans la même unité.
... ... ...
...
Un pourcentage indique une proportion par rapport à 100. Un pourcentage est un cas particulier de proportionnalité. Le coefficient de proportionnalité est une fraction dont le dénominateur est 100.
Le numérateur est appelé le taux du pourcentage.
| 25 % = |
25 100 |
- Pour calculer le pourcentage d’un nombre différent de 100, on peut multiplier le nombre par le taux du pourcentage et diviser le résultat par 100.
| 25 % de 500 = |
25 x 500 100 |
= |
12 500 100 |
= 125 |
Exemple :
Dans un école, il y a 45 % (45 pour cent) de garçons.
(Cela signifie donc que si l’on prend un groupe représentatif de 100 élèves de cette école, il y aura 45 garçons.)
Il y a 260 élèves dans cette école.
| 45 % de 260 = |
45 x 260 100 |
= |
11 700 100 |
= 117 |
Le nombre de garçons est donc de 117.
... ... ...
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le cycle 3 en mathématiques
CM1 - CM2
Calcul avec des décimaux - Calcul avec des fractions- La proportionnalité