


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie
... ... ...
 |
 |


... ... ...
...
| Triangles | Carrés | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Rappels Construction Propriétés |
Rappels Construction Propriétés |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cercles |
|
Définitions Construction Propriétés |

...
Les triangles sont des figures géométriques à 3 côtés et 3 sommets.

...
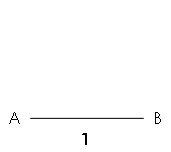
Pour construire un triangle, on utilise la règle graduée et le compas :
 |
 |
 |
 |
1./ Tracer avec la règle un côté du triangle (AB = 3 cm)
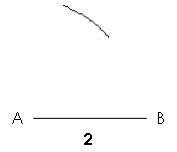
2./ Ouvrir le compas de la longueur d’un autre côté (AC = 3 cm), placer la pointe du compas sur l’extrémité du premier côté (A) et tracer un arc de cercle.
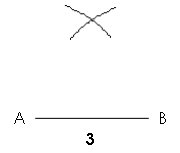
3./ Ouvrir le compas de la longueur du troisième côté (BC = 3 cm), placer la pointe du compas sur l’autre extrémité du premier côté (B) et tracer un nouvel arc de cercle.
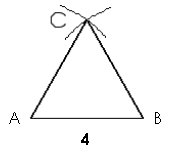
4./ Les arcs de cercle se coupent en 1 point (C). C’est le troisième sommet du triangle. Il ne reste plus qu’à tracer les deux côtés.
...
Construction des triangles particuliers
...
|
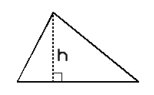
La hauteur La hauteur d’un triangle est la droite perpendiculaire à l’un des côtés et passant par le sommet opposé. |
 |
...
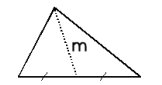 |
La médiane La médiane d’un triangle est la droite qui passe par le milieu d’un côté et le sommet opposé à ce côté. |
(Voir également : Niveau 3)
...
|
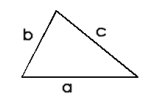
Le périmètre On calcule le périmètre d’un triangle en additionnant la mesure de ses 3 côtés. a + b + c |
 |
...
|
|
L’aire On calcule l’aire d’un triangle en multipliant la longueur de la base du triangle par sa hauteur correspondante, et on divise le résultat par 2. |
||
|
(a x h) 2 |
|||
...
... ... ...
...
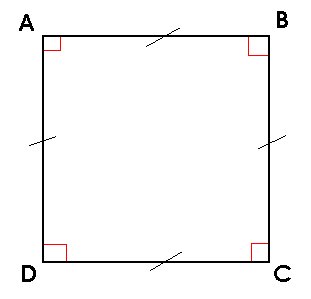
Les carrés sont des figures géométriques à 4 côtés égaux, 4 sommets et 4 angles droits.
...
Pour construire un carré, on utilise la règle graduée et l'équerre :
En commençant par les côtés :
 |
 |
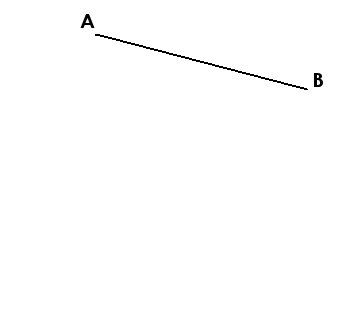
| 1./ Trace un segment [AB], de la longueur du côté du carré
... |
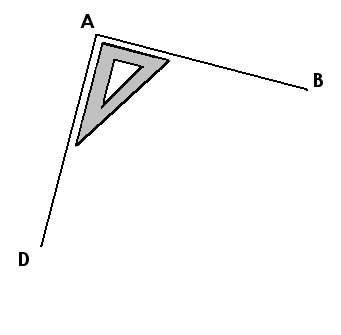
2./ Trace un segment [AD], perpendiculaire à [AB], de même longueur et passant par A
... |
 |
 |
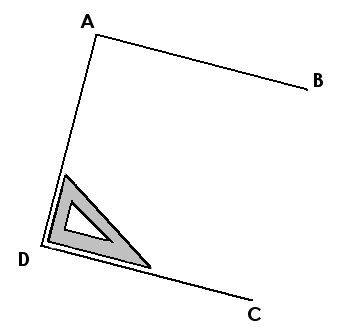
| 3./ Trace un segment [DC], perpendiculaire à [AD], de même longueur et passant par D ... |
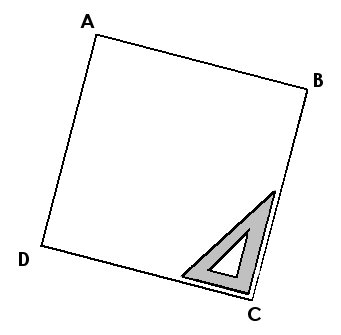
4./ Relie les points C et B, et vérifie que [BC] et [CD] sont perpendiculaires, ainsi que [AB] et [BC] ... |
...
En commençant par les diagonales :
 |
 |
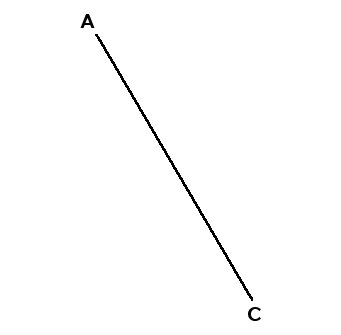
| 1./ Tracer un segment [AC], de la longueur de la diagonale du carré
... |
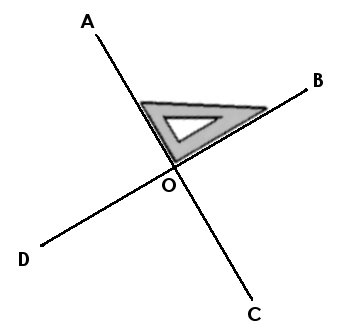
2./ Place le point O, milieu de [AC] et trace la droite perpendiculaire au segment [AC] passant par le point O. Puis place les points B et D tel que [AO] = [BO] = [CO] = [DO]
... |
 |
 |
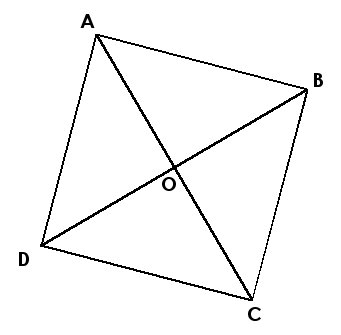
| 3./ Trace les segments [AB], [BC], [CD] et [DA]
... |
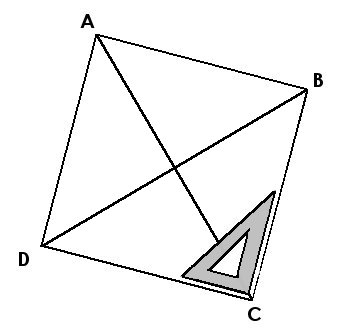
4./ Vérifie les 4 angles droits du carré avec ton équerre
... |
(Voir également : Niveau 3)
...
|
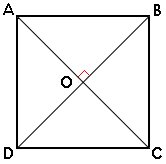
Les diagonales Les diagonales du carré sont les segments qui relient les sommets opposés. Elles sont de même longueur et se coupent perpendiculairement au centre du carré.
|
 |
...
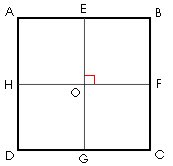 |
Les médianes Les médianes du carré sont les segments qui relient les milieux des côtés opposés. Elles sont de la même longueur que les côtés et se coupent perpendiculairement au centre du carré.
|
...
|
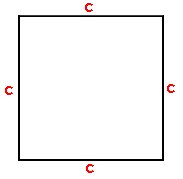
Le périmètre Pour calculer le périmètre d’un carré, il faut additionner la longueur des 4 côtés. c + c + c + c = 4 x c |
 |
...
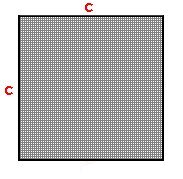 |
L'aire Pour calculer l’aire d’un carré, on multiplie entre elles les longueurs de 2 côtés consécutifs. c x c = c² |
...
... ... ...
...
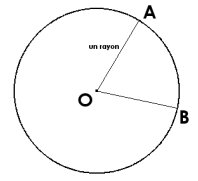
À partir d’un point (O), si je trace tous les points situés à une même distance (r) de ce point, j’obtiens un cercle de centre O.
La distance entre le centre du cercle et les points qui le constituent est appelée le rayon du cercle.
[OA], [OB] … sont des rayons du cercle de centre O et de rayon r.
...
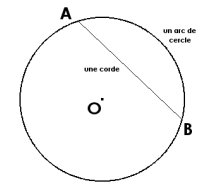
Soient A et B, deux points quelconque situés sur le cercle.
On appelle le segment [AB] une corde du cercle.
On appelle le morceau du cercle situé entre A et B un arc de cercle.
...
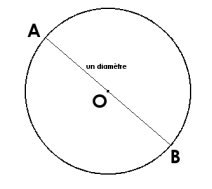
Tous les segments reliant 2 points différents du cercle et passant par le centre O sont appelés des diamètres du cercle.
...
Remarque :
La longueur du diamètre d’un cercle est égale à deux fois la longueur du rayon.
2 OA = 2 OB = OA + OB = AB
...
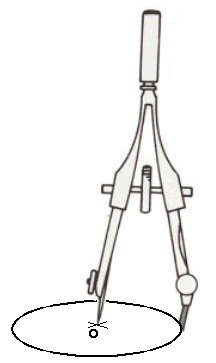
Pour tracer des cercles, on utilise un compas.
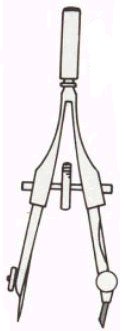 |
La première chose à faire est de régler l'écartement des branches du compas. Plus l'écartement est grand, et plus le cercle sera grand. Si l'on souhaite tracer un cercle d'un diamètre précis, alors il faut mesurer l'écartement du compas avec une règle. L'écartement du compas doit alors correspondre à la longueur du rayon du cercle. |
...
Ensuite, il faut placer précisément et enfoncer légèrement la pointe du compas à l'endroit ou se situe le centre du cercle. ... Enfin il faut faire pivoter le compas afin de tracer le cercle. ... Ceci n'est pas très facile au début !... Et il faut s'entrainer pour parvenir à tracer des cercles précis et nets !... |
 |
...
Pour calculer le périmètre d'un cercle, il faut connaitre la mesure du rayon de ce cercle et appliquer la formule suivante :
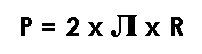
Avec ![]() (pi) = 3,14
(pi) = 3,14
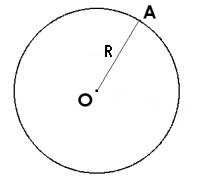
Exemple :
Soit un cercle de centre O et de rayon R (OA),
Si R = 5 cm
Alors le périmètre du cercle sera de :
P = 2 x 3,14 x 5 = 31,4 cm
...
La surface délimitée par un cercle s'appelle un disque.
Pour mesurer la surface d'un disque, on applique la formule suivante :
![]()
Avec ![]() (pi) = 3,14
(pi) = 3,14
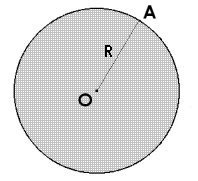
Exemple :
Soit un cercle de centre O et de rayon R (OA),
Si R = 5 cm
Alors l'aire du disque déterminé par le cercle sera de :
A = 3,14 x 5 x 5 = 78,4 cm²
... ... ...
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le cycle 3 en mathématiques
CM1 - CM2
Géométrie - Les triangles - Les carrés - Les cercles