


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie
... ... ...
 |
 |


... ... ...
...
| Rappels et compléments | Les solides |
|
Les triangles Propriétés Les quadrilatères Constructions |
Les solides usuels Les patrons |

...
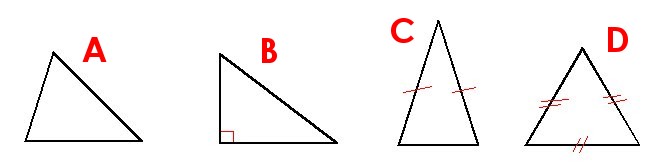
Les figures géométriques à 3 côtés et 3 sommets sont des triangles.
| Figures | Noms de la figure | Particularités |
| A | Le triangle quelconque | Aucune particularité |
| B | Le triangle rectangle | 1 angle droit |
| C | Le triangle isocèle | 2 côtés égaux |
| D | Le triangle équilatéral | 3 côtés égaux |
...
... ... ...
| Les médianes | Les médiatrices | Les hauteurs | Les bissectrices |
...
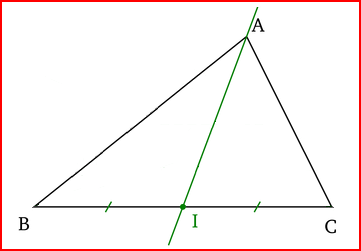
La médiane d'un triangle est une droite qui relie un sommet au milieu du côté opposé.
 |
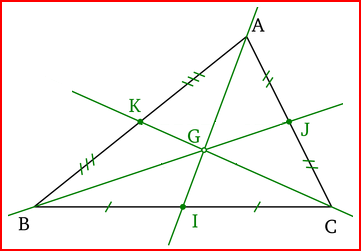 |
| I est au milieu de BC | J est au milieu de AC ; K est au milieu de AB |
Le point d'intersection des trois médianes d'un triangle est appelé centre de gravité (G).
...
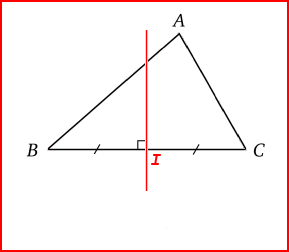
La médiatrice d'un triangle est une droite qui coupe le milieu d'un côté en formant un angle droit.
 |
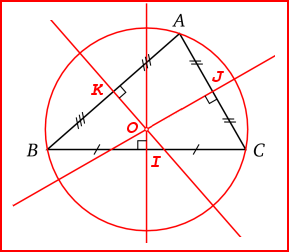 |
| I est au milieu de BC | J est au milieu de AC ; K est au milieu de AB |
Le point d'intersection des trois médiatrices d'un triangle est appelé centre du cercle circonscrit (0).
=> On peut tracer un cercle de centre O qui passe par les 3 sommets du triangle.
...
La hauteur d'un triangle est une droite qui passe par un sommet et qui coupe perpendiculairement le côté opposé.
 |
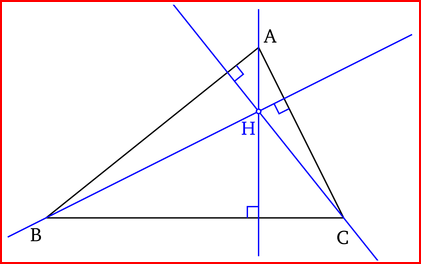 |
Le point d'intersection des 3 hauteurs d'un triangle est appelé orthocentre.
...
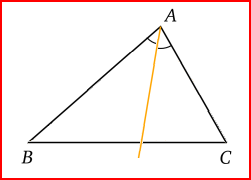
La bissectrice d'un triangle est une demi-droite qui partage un angle en deux angles de même mesure.
 |
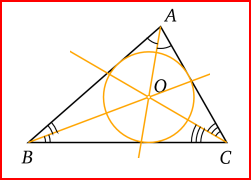 |
Le point d'intersection des trois bissectrices d'un triangle est appelé centre du cercle inscrit (0).
=> On peut tracer un cercle de centre O qui passe par les 3 côtés du triangle.
...
... ... ...
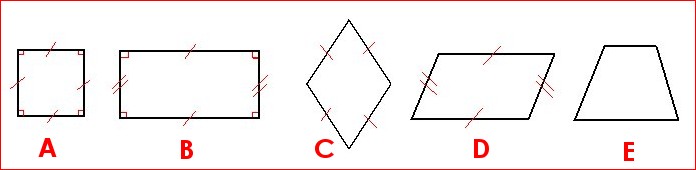
Les figures géométriques à 4 côtés et 4 sommets sont des quadrilatères.
| Figures | Noms de la figure | Particularités |
| A | Le carré | 4 côtés égaux et 4 angles droits |
| B | Le rectangle | Côtés égaux 2 à 2 et 4 angles droits |
| C | Le losange | 4 côtés égaux mais pas d'angle droit |
| D | Le parallélogramme | Côtés égaux 2 à 2 mais pas d'angle droit |
| E | Le trapèze | 2 côtés parallèles |
...
...
Constructions des quadrilatères particuliers
La construction des quadrilatères

...
... ... ...
...
Pour construire des solides les plus courants, on utilise les figures planes usuelles : les carrés, les rectangles, les triangles rectangles, les triangles isocèles et les triangles équilatéraux.
| Figures | Noms | Particularités |
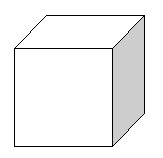 |
un cube |
- Nombre de faces : 6 - Nombre d'arêtes : 12 - Nombre de sommets : 8 - Nature des faces : 6 carrés |
 |
un parallélépipède |
- Nombre de faces : 6 - Nombre d'arêtes : 12 - Nombre de sommets : 8 - Nature des faces : 6 rectangles (ou 2 carrés et 4 rectangles) |
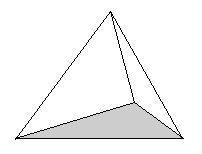 |
un tétraèdre |
- Nombre de faces : 4 - Nombre d'arêtes : 6 - Nombre de sommets : 4 - Nature des faces : 4 triangles équilatéraux |
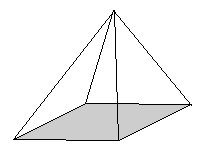 |
une pyramide |
- Nombre de faces : 5 - Nombre d'arêtes : 8 - Nombre de sommets : 5 - Nature des faces : 1 carré et 4 triangles isocèles (ou 1 rectangle et 4 triangles isocèles) |
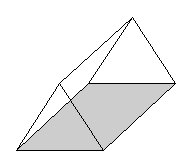 |
un prisme |
- Nombre de faces : 5 - Nombre d'arêtes : 9 - Nombre de sommets : 6 - Nature des faces : 2 triangles et 3 rectangles |
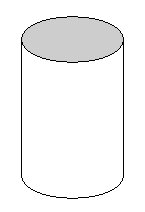 |
un cylindre |
- Nombre de faces : 3 - Nombre d'arêtes : 0 - Nombre de sommets : 0 - Nature des faces : 2 disques et 1 rectangle |
...
Pour construire un solide, il faut d'abord tracer un patron, regroupant les différentes faces du solide selon un agencement particulier.
Exemple :
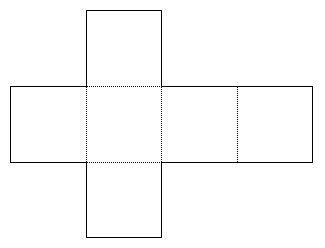
Le patron du cube :
Il est constitué de 6 carrés. Si l’on découpe et plie la figure selon les pointillés, on peut obtenir un cube.
Remarque :
Il existe d'autres solutions pour dessiner le patron du cube...
... ... ...
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le cycle 3 en mathématiques
CE2 - CM1
Géométrie - Les triangles - Les quadrilatères - Les solides