


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie
... ... ...
 |
 |


... ... ...
...
| Addition | Soustraction |
|
Propriétés Calcul d'une somme Applications |
Propriétés Calcul d'une différence Applications |
| Multiplication | Division |
|
Propriétés Calcul d'un produit Applications |
Propriétés Calcul d'un quotient Critères de divisibilité |

...
L'addition est une opération qui permet de calculer la somme de plusieurs nombres.
...
17 + 14 = 14 + 17
- On dit que l’addition est une opération commutative : on peut intervertir, ou commuter, les deux termes d’une somme sans changer la valeur de cette dernière.
Ainsi pour deux nombres quelconques a et b , on a :
a + b = b + a
...
2 + (98 + 129) = (2 + 98) + 129
- On dit que l’addition est une opération associative : on peut choisir l’ordre des calculs, associer les termes afin de se faciliter les calculs, lorsque la somme est de plus de deux nombres.
Ainsi pour trois nombres quelconques a, b et c, on a :
(a + b) + c = a + (b + c)
...
34 + 0 = 0 + 34 = 34
- On dit que l’addition possède un élément neutre : le 0
Ainsi quel que soit le nombre a, on a :
a + 0 = 0 + a = a
...
- Pour additionner des nombres, on dispose les termes l’un au-dessous de l’autre en alignant en colonnes les chiffres des unités, les chiffres des dizaines, les chiffres des centaines...
- Puis on ajoute les chiffres, colonne par colonne, à partir de la droite et l’on reporte une retenue lorsque la somme des chiffres est supérieure à 10.
Exemples :
|
1 4 5 + 5 2 1 9 7 |
1815 7 + 2 6 5 1 1 2 2 |
|
...
| Forme algébrique | Forme numérique | Problèmes associés |
| a + b = c | 5 + 7 = 12 | Pierre avait 5 billes au début de la journée. Il joue pendant la récréation et en gagne 7. Il en a donc 12 à la fin de la journée. |
| a + b = ? | 25 + 20 = ? | Natacha a 25 euros dans sa tirelire. Pour son anniversaire son grand-père lui donne un billet de 20 euros. - Quelle somme d'argent possède-t-elle maintenant ? |
| a + ? = c | 148 + ? = 200 | Jacques possède 148 timbres dans sa collection. Son oncle Albert lui en donne plusieurs et quand Jacques les compte à nouveau, il s’aperçoit qu’il en a maintenant 200. - Combien son oncle lui en a-t-il donnés ? |
| ? + b = c | ? + 35 = 2024 | Nous sommes en 2024 et Fanny a 35 ans. - En quelle année est-elle née ? |
...
L'addition et la soustraction sont deux opérations étroitement liées :
Ainsi pour résoudre des équations de la forme :
| a + ? = c | ou | ? + b = c |
Il faut calculer les soustractions suivantes :
| c - a = ? | ou | c - b = ? |
...

...
... ... ...
...
La soustraction est une opération qui permet de calculer la différence entre deux nombres.
...
10 - 7 ≠ 7 - 10
- La soustraction n’est pas commutative.
...
10 - 10 = 0
- La différence de deux nombres égaux est égale à zéro.
Si la différence de deux nombres est égale à zéro, alors ces deux nombres sont égaux.
Ainsi quel que soit le nombre a, on a :
a - a = 0
...
10 - 8 = (10 + 5) - (8 + 5) = 15 - 13 = 2
- Si on ajoute le même nombre aux deux termes d'une soustraction, la différence reste la même.
Ainsi pour 3 nombres quelconques a, b et c, on a :
a - b = (a + c) - (b + c)
...
10 - 7 = 3 => 3 + 7 = 10
- On peut facilement vérifier le résultat d'une soustraction en calculant l'addition associée.
C'est calculer la preuve de la soustraction.
Ainsi pour 3 nombres quelconques a, b et c, on a :
a - b = c => b + c = a
...
- Pour soustraire deux nombres, on dispose les termes l’un au-dessous de l’autre en alignant en colonne les chiffres des unités, les chiffres des dizaines, les chiffres des centaines...
- Puis on soustrait les chiffres, colonne par colonne, à partir de la droite et l’on reporte une retenue lorsque cela est nécessaire.
- Le calcul de la preuve permet de vérifier rapidement le résultat.
Exemples :
|
114 5 - 1 5 2 0 9 3 |
815 7 - 12 6 5 5 9 2 |
|
Calcul des preuves :
|
9 3 + 5 2 1 4 5 |
15 9 2 + 2 6 5 8 5 7 |
|
...
| Forme algébrique | Forme numérique | Problèmes associés |
| a - b = c | 9 - 3 = 6 | Jessim avait 9 billes au début de la journée. Il joue pendant la récréation et en perd 3. Il lui en reste donc 6 à la fin de la journée. |
| a - b = ? | 35 - 20 = ? | Nathalie a reçu 35 euros pour son anniversaire. Elle s'achète un beau livre coûtant 20 euros. - Combien lui reste-t-il dans sa tirelire ? |
| a - ? = c | 200 - ? = 150 | Rémi possède une collection de 200 petites voitures. Il décide d’en donner une partie à son petit frère. Quand il recompte ses voitures, Rémi en trouve 150. - Combien de petites voitures a-t-il données à son frère ? |
| ? - b = c | ? - 5 = 14 | Mélissa collectionne les poupées. Elle décide de donner 5 poupées à sa petite sœur. Quand elle recompte ses poupées, elle n’en a plus que 14. - Combien de poupées avait-elle avant d’en donner à sa sœur ? |
...
L'addition et la soustraction sont deux opérations étroitement liées :
Ainsi pour résoudre des équations de la forme :
| a - ? = c | ou | ? - b = c |
Il faut calculer les opérations suivantes :
| a - c = ? | ou | c + b = ? |
...
...
... ... ...
...
La multiplication est une opération qui permet de calculer le produit entre deux nombres.
...
15 x 12 = 12 x 15
- Nous disons que la multiplication est une opération commutative ; nous pouvons intervertir, ou commuter, les deux termes d’un produit sans changer la valeur de ce dernier.
Ainsi pour deux nombres quelconques a et b , on a :
a x b = b x a
...
2 x (6 x 5) = (2 x 6) x 5
- Nous disons que la multiplication est une opération associative ; nous pouvons choisir l’ordre des calculs, associer les termes afin de se faciliter les calculs, lorsque le produit est de plus de deux nombres.
Ainsi pour trois nombres quelconques a, b et c, on a :
(a x b) x c = a x (b x c)
...
34 x 0 = 0 x 34 = 0
- Nous disons que la multiplication possède un élément absorbant : le 0
Ainsi quel que soit le nombre a, on a :
a x 0 = 0 x a = 0
...
34 x 1 = 1 x 34 = 34
- Nous disons que la multiplication possède un élément neutre : le 1
Ainsi quel que soit le nombre a, on a :
a x 1 = 1 x a = a
...
- Pour calculer le produit de deux nombres, on dispose les termes l’un au-dessous de l’autre en les alignant vers la droite.
- Puis on multiplie les chiffres, un par un, à partir de la droite et l’on reporte une retenue lorsque cela est nécessaire.
- Lorsque le multiplicateur est un nombre composé de plusieurs chiffres, on effectue les calculs chiffre après chiffre en allant à chaque fois à la ligne, sans oublier de décaler les résultats !!!...
Exemples :
|
19 3 x 5 4 6 5 |
5 9 x 2 5 2 9 5 + 1 1 8 . 1 4 7 5 |
4 1 |
... ... ...
| Forme algébrique | Forme numérique | Problèmes associés |
| a x b = c | 3 x 28 = 84 | L'enseignant distribue 3 cahiers à chacun de ses 28 élèves. Il a distribué 84 cahiers. |
| a x b = ? | 3 x 5 = ? | Mathieu a acheté 3 pochettes de cartes. Chaque pochette contient 5 cartes. - Combien a-t-il acheté de cartes ? |
| a x ? = c | 5 x ? = 30 | Océane achète pour 30 centimes de bonbons à la boulangerie. Elle ne paie qu'avec des pièces de 5 centimes. - Combien de pièces doit-elle donner ? |
| ? x b = c | ? x 4 = 32 | Un coureur a parcouru 4 tours d'un circuit. En tout, il a parcouru 32 km. - Combien mesure le circuit ? |
...
La multiplication et la division sont deux opérations qui sont étroitement liées :
Ainsi pour résoudre des équations de la forme :
| a x ? = c | ou | ? x b = c |
Il faut calculer les divisions suivantes :
| c : a = ? | ou | c : b = ? |
...

...
... ... ...
...
La division est une opération qui permet de partager un nombre en un certain nombre de parties égales, avec un reste éventuel.
...
On appelle le dividende (D) le nombre que l'on souhaite partager,
le diviseur (d) est le nombre de parts,
le quotient (q) est le résultat de la division,
sans oublier le reste (r).
Le signe ":" est le symbole de la division.
Exemple :
12 : 5 = 2 et il reste 2
D : d = q + r
Dividende : diviseur = quotient + reste
...
10 : 5 ≠ 5 : 10
- La division n’est pas commutative.
...
10 : 10 = 1
- La division de deux nombres égaux est égale à 1.
Ainsi quelque soit le nombre a, on a :
a : a = 1
...
28 : 7 = 4 => 28 = 4 x 7
28 : 5 = 5 reste 3 => 28 = (5 x 5) + 3
- Le dividende est égal au produit du quotient et du diviseur, auquel on ajoute le reste.
On a ainsi :
D = (d x q) + r
Cette propriété est très utile pour vérifier le résultat d'une division.
...
Technique opératoire : la division en colonnes

...
- Pour poser une division, on commence par écrire le dividende et le diviseur, séparé par un trait vertical.
Puis on souligne le diviseur, afin de le séparer du quotient.
Exemple 1
328 : 5 = ?
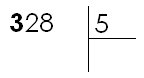 |
Le diviseur (5) a 1 chiffre ; on considère donc le premier chiffre du dividende (328), donc 3. |
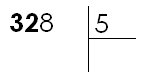 |
3 étant inférieur à 5, il faut prendre un deuxième chiffre au dividende, donc 32. |
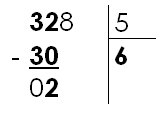 |
On divise donc 32 par 5. Le résultat est 6. (Dans 32, combien de fois 5 ? => 6) On écrit 6 sous le diviseur et on écrit le produit de 5 par 6 (soit 30) au-dessous de 32. Puis il faut soustraire 30 de 32. On obtient 2. |
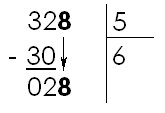 |
On abaisse ensuite le chiffre suivant du dividende (8) . |
 |
On divise maintenant 28 par 5. Le résultat est 5. (Dans 28, combien de fois 5 ? => 5) On écrit 5 sous le diviseur et on écrit le produit de 5 par 5 (soit 25) au-dessous de 28. Puis il faut soustraire 28 de 25. On obtient 3. Tous les chiffres du dividende ayant été utilisés, la division est terminée. |
On obtient la valeur approchée par défaut du quotient de 328 par 5 ; c'est 65 ;
... et le reste est égal à 3.
328 : 5 = 65 reste 3
ou
328 = (5 x 65) + 3
... ... ...
Exemple 2
1 287 : 24 = ?
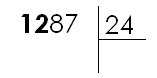 |
Le diviseur (24) a 2 chiffres ; on considère donc les deux premiers chiffres du dividende (1 287), donc 12. |
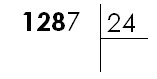 |
12 étant inférieur à 24, il faut prendre un troisième chiffre au dividende, donc 128. |
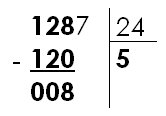 |
On divise donc 128 par 24. Le résultat est 5. (Dans 128, combien de fois 24 ? => 5) On écrit 5 sous le diviseur et on écrit le produit de 24 par 5 (soit 120) au-dessous de 128. Puis il faut soustraire 120 de 128. On obtient 8. |
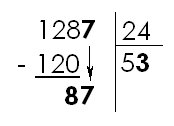 |
On abaisse ensuite le chiffre suivant du dividende (7). On divise maintenant 87 par 24. Le résultat est 3. (Dans 87, combien de fois 24 ? => 3) On écrit 3 sous le diviseur. |
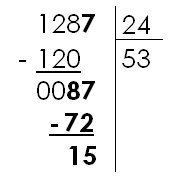 |
Puis on écrit le produit de 3 par 24 (soit 72) au-dessous de 87. Puis il faut soustraire 72 de 87. On obtient 15. Tous les chiffres du dividende ayant été utilisés, la division est terminée. |
On obtient la valeur approchée par défaut du quotient de 1 287 par 24 ; c'est 53 ;
... et le reste est égal à 15.
1 287 : 24 = 53 reste 15
ou
1 287 = (24 x 53) + 15
Remarques :
- Le reste ne peut jamais être supérieur au diviseur.
- Quand le diviseur est un nombre à 2 chiffres ou plus, il est pratique de construire la table de multiplication de ce nombre avant d'effectuer la division.
... ... ...
| Forme algébrique | Forme numérique | Problèmes associés |
| a : b = c | 84 : 3 = 28 | Trois amis mangent au restaurant et décident de partager l'addition totale de 84 euros. Chaque ami doit payer 28 euros. |
| a : b = ? | 30 : 2 = ? | Damien et son frère ont un sac contenant 30 billes qu'ils souhaitent se partager équitablement. - Combien chaque enfant aura-t-il de billes ? |
| a : ? = c | 48 : ? = 8 | Le fermier amène 8 boîtes d'oeufs au marché. Ses poules ont pondu 48 oeufs ce matin. - Combien y a-t-il d'oeufs dans chaque boîte ? |
| ? : b = c | ? : 4 = 7 | Isabelle a donné 7 bonbons à chacun de ses 4 enfants. - Combien avait-elle de bonbons avant de les partager ? |
...
La division et la multiplication sont deux opérations qui sont étroitement liées :
Ainsi pour résoudre des équations de la forme :
? : b = c
Il faut calculer la multiplication suivante :
c x b = ?
... ... ...
Il peut être intéressant de connaitre certains critères de divisibilité.
Critère de divisibilité par 2 :
- Un nombre entier naturel est divisible par 2 s’il est pair, c’est à dire si son chiffre des unités est 0 ; ou 2 ; ou 4 ; ou 6 ; ou 8.
Exemple :
Le nombre 358 est divisible par 2 parce que son chiffre des unités est 8 ;
358 : 2 = 174
...
Critère de divisibilité par 3 :
- Un nombre entier naturel est divisible par 3 si le nombre à un chiffre obtenu en calculant la somme des chiffres du nombre initial, puis la somme des chiffres de la somme formée, etc. est 3 ; ou 6 ; ou 9.
Exemple :
Le nombre 279 est divisible par 3 ; en effet :
2 + 7 + 9 = 18 et 1 + 8 = 9;
279 : 3 = 93
...
Critère de divisibilité par 4 :
- Un nombre entier naturel est divisible par 4 si ses deux derniers chiffres sont divisibles par 4. Ce nombre est deux fois divisible par 2.
Exemple :
Le nombre 6 548 est divisible par 4 ; en effet :
48 est dans la table de 4 => 4 x 12 = 48;
6 548 : 4 = 1 637
...
Critère de divisibilité par 5 :
- Un nombre entier naturel est divisible par 5 si le chiffre des unités est 0 ou 5.
Exemple :
Le nombre 855 est divisible par 5 puisqu'il se termine par 5.
855: 5 = 171
...
Critère de divisibilité par 6 :
- Un nombre entier naturel est divisible par 6 s’il est divisible par 2 et par 3.
Exemple :
Le nombre 276 est divisible par 2 et par 3, donc par 6 ;
276 : 6 = 46
...
Critère de divisibilité par 9 :
- Un nombre entier naturel est divisible par 9 si le nombre à un chiffre obtenu en calculant la somme de ses chiffres, puis en répétant l’opération jusqu’à ce qu’il n’y ait plus qu’un chiffre, est 9.
Exemple :
Le nombre 675 est divisible par 9, car : 6 + 7 + 5 = 18 et 1 + 8 = 9
675 : 9 = 75
...
Critère de divisibilité par 10 :
- Un nombre entier naturel est divisible par 10 si le nombre des unités est égal à 0.
Exemple :
Le nombre 9 240 est divisible par 10 ;
9 240 : 10 = 924
...
...

... ... ...
... ... ...
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le cycle 3 en mathématiques
CE2 - CM1
Calcul - L'addition - La soustraction - La multiplication - La division