


 |
 |
 |
Numération - Calcul - Problèmes - Mesures - Géométrie
... ... ...
 |
 |


... ... ...
...
| Les longueurs | Les aires |
|
Les unités Les conversions |
Les unités Les conversions Formulaire |
| Les capacités | Les masses |
|
Les unités Les conversions Formulaire |
Les unités Les conversions |
| Les durées |
|
Les unités Les conversions Les calculs |

Pour mesurer des distances, on utilise les unités de mesure de longueur.
Le mètre (m) est l’unité principale, mais on utilise également ses multiples (dam, hm, km) et ses sous-multiples (dm, cm, mm).
Pour exprimer une mesure de longueur, on choisit toujours l’unité de mesure la plus cohérente. Ainsi, par exemple, on exprimera la distance entre deux villes avec les kilomètres, et la taille d’une fourmi avec les millimètres.
...

...
Pour effectuer des conversions avec des unités de longueur, on peut reproduire et utiliser un tableau similaire à celui-ci :

Lecture du tableau :
Ligne 1 : 1 mètre (ou 10 dm ou 100 cm ou 1 000 mm)
Ligne 2 : 2,05 mètres (ou 20,5 dm, ou 205 cm, ou 2 050 mm)
Ligne 3 : 8,5 kilomètres (ou 85 hm, ou 850 dam, ou 8 500 m)
Ligne 4 : 80,5 mètres (ou 8,05 dam ou 805 dm, ou 8 050 cm)
...
Conversion des mesures de longueur
(Voir également : Niveau 3)
...
...
... ... ....
On peut déterminer l’aire, l’étendue ou la superficie d’une surface plane.
Pour cela, il faut rechercher le nombre d’unités d’aire qu’elle contient, ou bien encadrer l’aire recherchée par 2 autres surfaces dont on connait l’aire.
...
L’unité de base utilisée pour mesurer des aires est le mètre carré (m²), mais on utilise aussi ses multiples et sous-multiples :
- 1 mètre carré (m²) équivaut à la surface d’un carré dont les côtés mesurent 1 mètre.
- 1 centimètre carré (cm²) équivaut à la surface d’un carré dont les côtés mesurent 1 centimètre.
- 1 kilomètre carré (km²) équivaut à la surface d’un carré dont les côtés mesurent 1 kilomètre.
...
Multiples et sous-multiples du mètre carré

1 km² = 1 000 000 m²
1 hm² = 10 000 m²
1 dam² = 100 m²
1 dm² = 0,01 m²
1 cm² = 0,000 1 m²
1 mm² = 0,000 001 m²
...
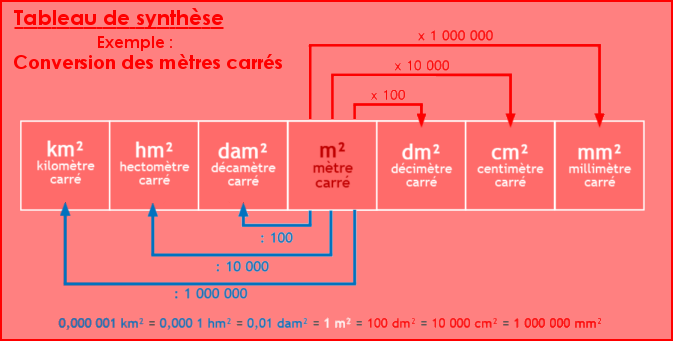
Pour convertir les unités d’aire, on peut utiliser un tableau de conversion.
(Attention !... Il faut remplir 2 cases par unité !...)

Lecture du tableau :
Ligne 1 : 1 cm² = 100 mm² = 0, 01 dm² = 0,000 1 m²
Ligne 2 : 0,5 m² = 50 dm² = 5 000 cm² = 500 000 mm²
Ligne 3 : 100 000 m² = 1 000 dam² = 10 hm² = 0,1 km²
Ligne 4 : 4,5 km² = 450 hm² = 45 000 dam² = 4 500 000 m²
...
...
Exemple : Convertir des mètres carrés
...
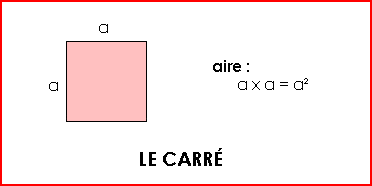
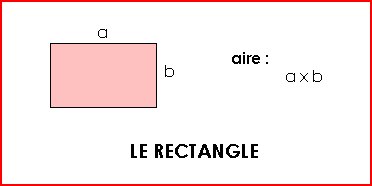
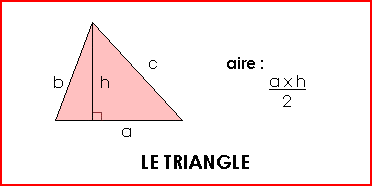
Pour calculer l'aire de certaines figures planes, il existe des formules :
 |
 |
|
Exemple : Mesure du côté (a) = 15 cm L'aire du carré est de : 15 x 15 = 225 cm² ... |
Exemple : Longueur (a) = 150 m et largeur (b) = 50 m L'aire du rectangle est de : 150 x 50 = 7 500 m² ... |
 |
 |
|
Exemple : Base (a) = 5 cm et hauteur (h) = 5 cm L'aire du triangle est de : (5 x 5) : 2 = 25 : 2 = 12,5 cm² ... |
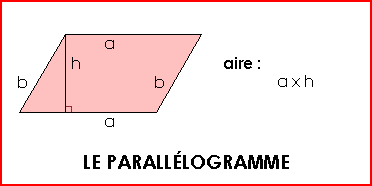
Exemple : Longueur (a) = 10 cm et hauteur (h) = 5 cm L'aire du parallélogramme est de : 10 x 5 = 50 cm² ... |
 |
 |
|
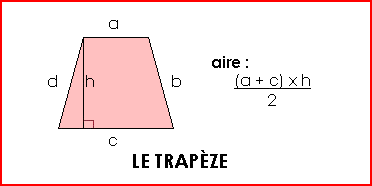
Exemple : Petite base (a) = 4 cm Grande base (c) = 7 cm Hauteur (h) = 5 cm L'aire du trapèze est de : [(4 + 7) x 5] : 2 = 55 : 2 = 27,5 cm² ... |
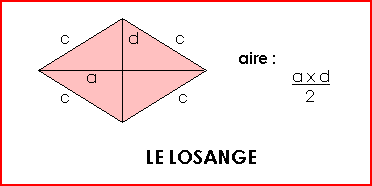
Exemple : Grande diagonale (a) = 10 cm Petite diagonale (d) = 6,5 cm L'aire du losange est de : (10 x 6,5) : 2 = 65 : 2 = 32,5 cm² ... |
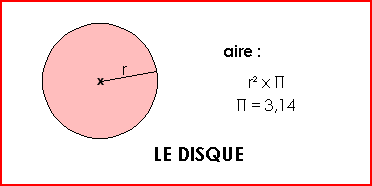
Exemple :
Rayon (r) = 5 cm
L'aire du disque est de : (5 x 5) x 3,14 = 25 x 3,14 = 78,5 cm²
... ... ...
...
...
... ... ...
Les mesures de capacité servent à mesurer des contenances.
La capacité d'un objet mesure la quantité de matière que peut contenir cet objet.
...
- Les capacités
Pour mesurer des capacités, on utilise des verres doseur (ou verres mesureur), des éprouvettes... sur lesquelles sont indiquées des graduations permettant de mesurer les quantités en fonction des différentes matières.
Les pompes à essence se servent également du litre comme unité de mesure.
 |
 |
 |
 |
| Des verres mesureur | Pompes à essence | ||
...
Le litre est l’unité principale des mesures de capacité.
C’est aussi la plus utilisée. Certaines unités ne sont que rarement employées (le décalitre, le décilitre, le millilitre).
À noter également que le kilolitre (unité qui correspond à 1 000 litres n’est plus du tout utilisée au profit du mètre cube, autre mesure de capacité, couramment employée aujourd’hui).
L’unité de base, le litre, équivaut à une masse d’un kilogramme d’eau, et correspond à un volume d’1 décimètre cube.
...
- Les volumes
On peut également déterminer le volume d’un objet en utilisant les unités de volume.
Pour cela, il faut rechercher le nombre d’unités de volume qu’il contient, ou bien encadrer le volume de l’objet recherché par le volume de 2 autres objets dont on connaît le volume.
- L’unité de base utilisée pour mesurer des volumes est le mètre cube (m3), mais on utilise aussi ses multiples et sous-multiples :
- 1 mètre cube équivaut au volume d’un cube dont les côtés mesurent 1 mètre.
- 1 centimètre cube équivaut au volume d’un cube dont les côtés mesurent 1 centimètre.
- 1 kilomètre cube équivaut au volume d’un cube d’1 kilomètre de côté…
...

...

1 km3 = 1 000 000 000 m3
1 hm3 = 1 000 000 m3
1 dam3 = 1 000 m3
1 dm3 = 0,001 m3
1 cm3 = 0,000 001 m3
1 mm3 = 0,000 000 001 m3
...
Conversions utiles :
| 1 L = 10 dL = 100 cL = 1 000 mL | 1 hL = 10 daL = 100 L |
...
1 m3 = 1 000 dm3 = 1 000 000 cm3 = 1 000 000 000 mm3
1 km3 = 1 000 hm3 = 1 000 000 dam3 = 1 000 000 000 m3
...
| 1 L = 1 dm3 | 1 000 L = 1 m3 | 1 mL = 1 cm3 |
...

Lecture du tableau :
Ligne 1 : 1 L = 10 dL = 100 cL = 1 000 mL
Ligne 2 : 20 hL = 200 daL = 2 000 L = 20 000 dL ...
Ligne 3 : 50 cL = 500 mL = 5 dL = 0,5 L
Ligne 4 : 1,5 L = 15 dL = 150 cL = 1 500 mL
...
(Attention !... Il faut remplir 3 cases par unité !...)

Lecture du tableau :
Ligne 1 : 1 m3 = 100 dm3 = 1 000 000 cm3 = 1 000 000 000 mm3
Ligne 2 : 0,5 km3 = 500 hm3 = 500 000 dam3 = 500 000 000 m3
Ligne 3 : 12,3 cm3 = 12 300 mm3 = 0,012 3 dm3
Ligne 4 : 750,5 m3 = 750 500 dm3 = 0,750 5 dam3
...
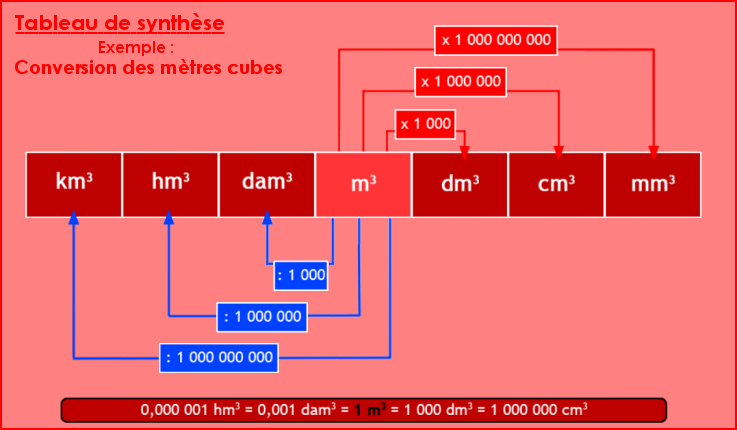
Exemple : Convertir des mètres cubes
...

Lecture du tableau :
Ligne 1 : 1 m3 = 10 hL = 100 daL = 1 000 L
Ligne 2 : 5,5 L = 5,5 dm3 = 55 dL = 5 500 cm3
Ligne 3 : 2 cL = 20 cm3 = 20 mL = 20 000 mm3
Ligne 4 : 8,5 m3 = 8 500 L
...
Attention dans les calculs à bien mettre les mesures dans la même unité !...
...
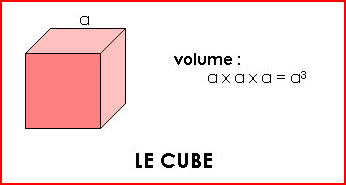
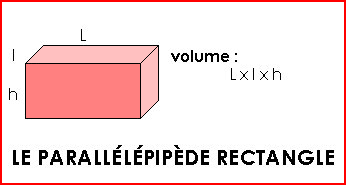
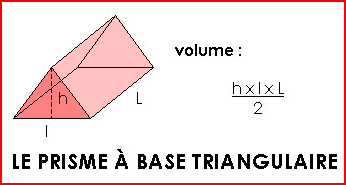
Pour calculer le volume de certains solides, il existe des formules :
 |
 |
|
Exemple : Côté (a) = 4 cm Le volume du cube est de : 4 x 4 x 4 = 64 cm3 ... |
Exemple : Longueur (L) = 10 cm Largeur (l) = 5 cm Hauteur (h) = 6 cm Le volume du parallélépipède est de : 10 x 5 x 6 = 300 cm3 ... |
 |
 |
|
Exemple : Longueur (L) = 10 cm Largeur (l) = 5 cm Hauteur (h) = 5 cm Le volume du prisme est de : (10 x 5 x 5) : 2 = 250 : 2 = 125 cm3 ... |
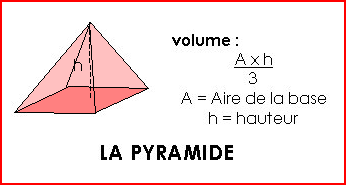
Exemple : Aire (A) = 12 cm² Hauteur (h) = 6 cm Le volume du tétraèdre est de : (12 x 6) : 3 = 72 : 3 = 24 cm3 ... |
 |
 |
|
Exemple : Aire (A) = 400 cm² Hauteur (h) = 15 cm Le volume de la pyramide est de : (400 x 15) : 3 = 6 000 : 3 = 2 000 cm3 ... |
Exemple : Rayon (R) = 3 cm Hauteur (h) = 10 cm Le volume du cylindre est de : 3,14 x 3 x 3 x 10 = 282,6 cm3 ... |
...
...
... ... ...
Les unités de masse servent à mesurer des quantités de matière.
La masse d'un objet mesure la quantité de matière qui constitue cet objet.
La masse d'un objet est la même quel que soit l'endroit où il se trouve dans l'univers. Il ne faut pas confondre la masse et le poids qui est la mesure de l'interaction de la masse et du champ de gravitation (le poids est une force).
L'unité de base de la masse est le kilogramme (kg) et non pas le gramme (g). On utilise également la tonne égale à 1 000 kg et le quintal, équivalent de 100 kg.
L’unité de base, le kilogramme, correspond à la masse exacte d’un litre d’eau.
...

1 quintal (q) = 100 kg
1 tonne (t) = 1 000 kg
...
Pour effectuer des conversions avec des unités de masse, on peut reproduire et utiliser un tableau similaire à celui-ci :

Lecture du tableau :
Ligne 1 : 1 kg (ou 10 hg ou 10 dag ou 1 000 g…)
Ligne 2 : 5 q (ou 500 kg, ou 0,5 t, ou 500 000 g...)
Ligne 3 : 8,5 g (ou 85 dg, ou 850 cg, ou 8 500 mg…)
Ligne 4 : 3,25 t (ou 32,5 q, ou 3 250 kg ou 3 250 000 g…)
...
Remarque :
Dans le langage courant, on utilise souvent le mot "poids" à la place du mot "masse".
...
...
... ... ...
|
1 millénaire = 1 000 ans 1 siècle = 100 ans 1 an = 365 jours |
1 semestre = 6 mois 1 trimestre = 3 mois 1 mois = 28, 29 ,30 ou 31 jours 1 semaine = 7 jours |
1 jour = 24 heures 1 heure = 60 minutes 1 minute = 60 secondes |
...
1 an = 12 mois = 365 jours = 8 760 heures = 525 600 minutes = 31 536 000 secondes
1 semaine = 7 jours = 168 heures= 10 080 minutes = 604 800 secondes
1 jour = 24 heures = 1 440 minutes = 86 400 secondes
Exemples :
1./ Convertir 9 ans 175 jours 13 heures 15 minutes 50 secondes en secondes :
1 an = (365 x 24 x 60 x 60) s = 31 536 000 secondes
=> 9 ans = 9 x 31 536 000 = 283 824 000 secondes
1 jour = 24 x 60 x 60 = 86 400 secondes
=> 175 jours = 175 x 86 400 = 15 120 000 secondes
1 heure = 60 x 60 = 3 600 secondes
=> 13 heures = 13 x 3 600 = 46 800 secondes
1 minute = 60 secondes
=> 15 minutes = 15 x 60 = 900 secondes
Donc 9 ans 175 jours 13 heures 15 minutes 50 secondes font :
283 824 000 + 15 120 000 + 46 800 + 900 + 50 = 298 991 750 secondes
...
2./ Convertir 1 milliard de secondes en années, mois, jours, heures et secondes :
1 000 000 000 : 60 = 16 666 666 minutes reste 40 secondes
16 666 666 : 60 = 277 777 reste 46
277 777 : 24 = 11 574 reste 1
11 574 : 365 = 31 reste 259
Donc 1 milliard de secondes = 31 ans, 259 jours, 1 heure, 46 minutes et 40 secondes.
...
Pour effectuer des calculs avec les unités de temps, il faut faire attention aux unités !...
Exemples :
L'addition |
La soustraction |
| ... | ... |
La multiplication |
La division |
...
... ... ...
 |
 |
 |
 |
 |

 |
 |
... ... ...
 |
 |
 |
 |
 |
Cours théoriques pour le cycle 3 en mathématiques
CM1 - CM2
Mesures - Les longueurs - Les aires - Les capacités - Les masses - Les durées